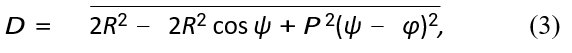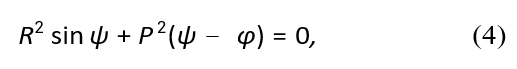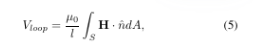Возможности литцендрата с использованием метода быстрого цифрового реалистичного моделирования

Реалистичная симуляция возможностей литцендрата с помощью цифрового метода моделирования

Аннотация— Практическое обоснование потерь многожильных проводов с учетом их конструкции. В исследовании использована процедура, которая помогает определить потери энергии, вызванные током и магнитным полем. Это метод быстрого цифрового реалистичного моделирования. В нашей работе мы оцениваем колебания потерь в одно- и двухслойных многожильных проводах в зависимости от шага скручивания в широком диапазоне значений, а также с небольшим шагом. Представлено экспериментальное подтверждение предположений, сделанных с помощью цифровой симуляции. Результаты подтверждают качество цифровых методов в предоставлении ценных данных о реальной конструкции литцендрата.

I. Введение

Эффективность высокочастотных силовых магнитных компонентов зачастую может быть улучшена за счет использования литцендрата, который состоит из небольших изолированных жил, сплетенных или скрученных для распределения плотности тока по всей площади поперечного сечения провода, как показано на рис. 1.

Мы решили провести данное исследование, чтобы оценить предлагаемое снижение потерь и соответствующим увеличением затрат при использовании многожильного провода вместо обычного кабеля. [1]. Стоимость литцендрата продиктована его конструкцией, но даже просто скрученные нити могут обеспечить значительное преимущество. Фактически мы видим, что даже скрученные жилы из неизолированной меди могут обеспечить значительное снижение потерь по сравнению со сплошным проводом [2].

Однако основная проблема оптимизации конструкции литцендрата связана с трудностью количественной оценки достижимого снижения потерь. Процедуры экспериментального определения характеристик, подобные описанным в [3], требуют сложного испытательного оборудования, а также изготовления и подготовки множества образцов литцендрата в широком диапазоне конструктивных параметров. С другой стороны, трехмерное цифровое моделирование общего назначения бывает очень дорогостоящим, требующим использования «высокопроизводительных вычислений [с] с помощью предоставленных компьютерных ресурсов» [4]. Поэтому существующая оптимизация литцендрата по большей части сосредоточена на балансировке количества жил, где внимание сосредоточено на идеальной конструкции многожильности, успешно выравнивающей ток через каждую жилу [1], [5], [6].

В этой статье мы описываем вычислительную процедуру для характеристики потерь в существующих конструкциях из литцендратной проволоки с помощью недавно представленного инструмента быстрого цифрового моделирования.

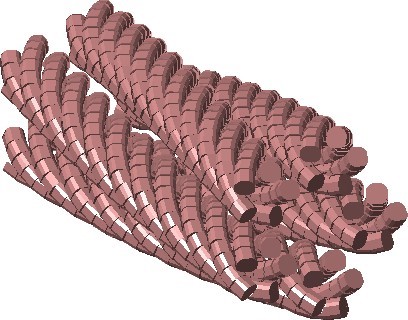
Рисунок 1: Круглая конструкция литцендрата рекурсивно скручивает жилы проволоки в пучки, а пучки проволоки в более крупные пучки, в результате чего получается схема, позволяющая каждой жиле проходить все радиальные и азимутальные положения в поперечном сечении проволоки.

в [7]. Существующая теория, которая лежит в основе предшествующих оптимизаций литцендрата, вычисляет потери как сумму двух компонентов, один из которых обусловлен протеканием чистого тока, а другой — внешним магнитным полем [8]. Мы расширяем этот подход, моделируя оба механизма потерь для моделей многожильного провода, которые включают основные детали конструкции. Используя высокоскоростной метод, мы изучили шаг проводов в широком диапазоне значений, выявив ряд данных в конструкции провода. Предположения подтверждаются экспериментальными измерениями.

II. ПРЕДПОСЫЛКИ

A. Теория потерь энергии

В области силовой электроники принято связывать потери энергии в высокочастотных проводниках состоящими из двух примерно-ортогональных составляющих, с скин-эффектом и эффекома близости [8], например,

Ptot(f ) = Pskin(f ) + Pprox(f ). (1)

Первый термин обычно используется для самоиндуцированных потерь на вихревые потоки. Последний термин обычно относится к потерям на вихревые токи, вызванным внешними магнитными полями, например, рассеянными магнитными полями от соседних витков или от магнитного сердечника. Оба термина включают вихревые токи, которые циркулируют внутри нитей, и вихревые токи, которые циркулируют между разными нитями. Согласно этому описанию, мы можем записать компоненты как в конечном счете управляемые соответственно чистой величиной тока I и величиной внешнего магнитного поля |H|, например,

Pskin(f ) = F (f )I2Rdc, Pprox(f ) = G(f )

где F и G — важные параметры, которые полностью описывают частотную зависимость материала провода, определяемую на единицу длины для среднеквадратичных или пиковых значений I и H. Это простое уравнение является основным строительным блоком для уравнений потерь во всех видах устройств, состоящих из скрученных проводников. Заинтересованный читатель может обратиться к [8]–[10] за подробностями о выводах и применении.

Два геометрических коэффициента, F и G, являются важными параметрами, которые характеризуют конкретный материал и конструкцию проволоки. Коэффициент F представляет собой безразмерную величину, также известную как Rac/Rdc,. коэффициент сопротивления переменного/постоянного тока. Он измеряет частотную зависимость сопротивления в одиночном изолированном проводе — в очень большом контуре или в теоретическом пределе, простирающемся от бесконечности до бесконечности. Коэффициент G обозначает магнитные диффузионные потери, он выражен в единицах ватт на А/м в квадрате на единицу длины, и измеряет потери, индуцированные в материале провода, когда на него воздействует единичное однородное возбуждение магнитного поля в поперечном направлении.

Хорошо известны точные решения для F в одножильном круглом проводе, а также для G, если предположить, что внешнее магнитное поле является поперечным, однородным и однородным по проводу [8], [11]. Эти решения дают нам почти конечные значения F и G в пучках многожильных проводов, таких как литцедрат, при условии, что каждая жила несет одинаковое распределение тока внутри жгута. Если провода намотаны зигзагообразно, возможно, в окне сердечника электромагнита, все поперечное сечение обмотки можно рассматривать как область однородной плотности тока, и можно получить похожие конечные значения. [5], [ 9]. (а) (б)

Выраженное в формуле решение предоставили разработчикам силовой электроники, а также ценную информацию о лежащей в основе данных физических процессов потерь энергии, а затем были широко использованы в оптимизации выбора правильного провода для каждого объекта. Однако очень мало известно о том, как следует скручивать провод для достижения постоянной плотности тока, которая просто предполагалась при выводе этих уравнений. Более того, если образец литцендрата отклоняется от идеальной конструкции — по ошибке или намеренно — эти уравнения сильно теряют в прогнозировании, и проектировщику приходится прибегать к экспериментальным методам.

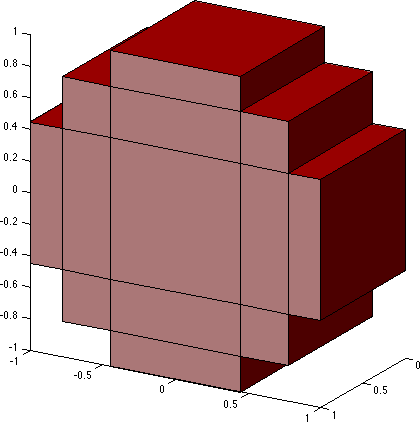
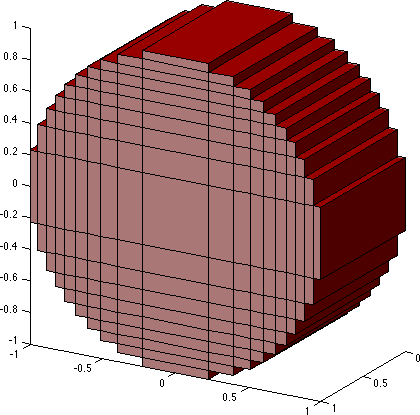
Рисунок 2: Оцифровка нити в методе эквивалентной схемы с частичным элементом. Параметр дискретизации (оцифровки) (a) 3; и (b) 10.

B. Быстрое цифровое моделирование

Цифровое моделирование может устранить многие недостатки аналитических уравнений и использоваться для анализа неидеальной конструкции. Однако, происходит значительное увеличение объема вычислений, поэтому необходимо выбрать наиболее эффективный метод для рассматриваемой задачи.

Моделирование в этой статье было выполнено с использованием метода, представленного в [7], основанного на интегральной формулировке уравнений Максвелла, более известной как метод эквивалентной схемы с частичными элементами (PEEC) [12], [13]. По сути, метод PEEC преобразует электромагнитную задачу в задачу эквивалентной схемы, разделяя проводящий объем электромагнитной задачи по длине и поперечному сечению в нити с током, как показано на рис. 2, позволяя волокнам взаимодействовать через собственные и взаимные индуктивности [12], [14]. Метод нашел широкое применение при анализе микроэлектроники и межсоединений [13], [15]. Наш PEEC похож на метод FastHenry [13] (не нашла в интернете, что такое – прим. пер.), но оптимизациями в скорости и точности, характерными для задач с проводами и возбуждением магнитного поля [7].

Эффективность вычислений метода PEEC достигается за счет ограничения объемной сетки только токопроводящим материалом при неявном учете наличия окружающего свободного пространства. Обычно это приводит к уменьшению числа неизвестных в 10–100 раз (пример см. в [16]). Этот метод особенно эффективен для энергетических объектов, потому что проводники, такие, например, как отдельные жилы в пучке литцендрата, обычно имеют тщательно подобранные размеры в соответствии с толщиной скин-слоя. Ограничение анализа только частотами с разумными потерями позволяет нам использовать относительно крупную сетку в проводнике без ущерба для точности.

Мы иллюстрируем точность и скорость метода для литцедрата через соотношения точного моделирования с размером сетки проводника. Задача состоит в том, чтобы правильно предположить Fф одножильного провода с AWG 38, который имеет известное точное решение [11].

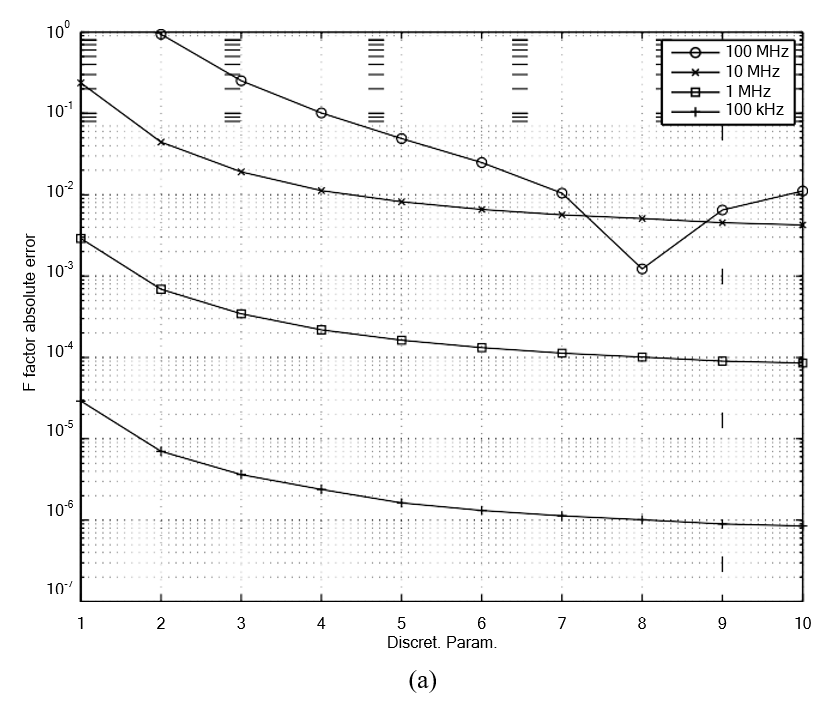
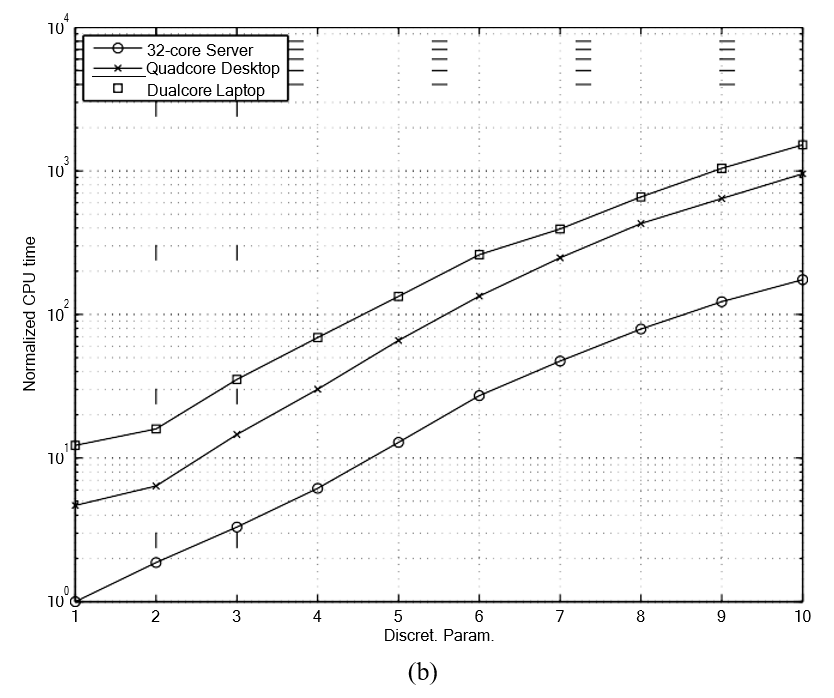
Рисунок 3: (а) Абсолютная погрешность F и (б) усреднение моделирования для различных уровней дискретизации. Обратите внимание, что поскольку F = 1, его абсолютная ошибка того же порядка, что и относительная ошибка. Моделирование проводилось для одножильного провода AWG 38. Радиус нити соответствует глубине ее скин-слоя на частоте 1,75 МГц.

Провод имеет диаметр 0,101 мм, а глубина скин-слоя соответствует радиусу провода на частоте 1,75 МГц. По длине провод делится не менее чем на 20 сегментов для прямых участков и не менее чем на 12 сегментов на шаг длины для криволинейных участков. Сетки поперечного сечения показаны на рис. 2, где сетка создается с использованием квадратичного правила, а «параметр дискретизации» определяется как количество элементов по радиусу круглого поперечного сечения, включая центральный элемент. Прямоугольные элементы в форме кирпича использовались для максимизации скорости вычислений [7].

Были протестированы три компьютерные платформы: двухъядерный ноутбук с частотой 2,1 ГГц, четырехъядерная настольная рабочая станция с частотой 2,5 ГГц и двухпроцессорный 32-ядерный вычислительный сервер с частотой 3 ГГц.

Как показано на рис. 3, ошибка прогноза уменьшается логарифмически с точностью дискретизации, но время моделирования также увеличивается логарифмически. Если требуется точный прогноз для частоты 100 МГц или даже 10 МГц, то вычислительная нагрузка будет весьма значительной. Однако жгут литцендрата, изготовленный из провода AWG 38, рекомендуется только для частот от 50 кГц до 100 кГц [17], и даже в этом случае только для недорогих конструкций с высокими потерями в этом диапазоне частот с помощью таких методов оптимизации, как [1], [5]. Ограничение частоты развертки до 1 МГц, даже при уровне дискретизации 2 и всего пяти элементах на поперечное сечение достаточно для достижения ошибки прогнозирования ниже 0,1%. Уменьшение дискретности с 7 до 2 приводит к ускорению в 50-100 раз на всех трех протестированных платформах на рис. 3б. Чтобы представить это в перспективе, решение тестовой задачи, дискретизированной до уровня 2, на двухъядерном ноутбуке было в 4-5 раз быстрее, чем решение той же задачи, дискретизированной до уровня 7, на 32-ядерном вычислительном сервере. Чтобы сбалансировать компромисс между скоростью и точностью, все остальные вычисления в этой статье были выполнены с уровнем дискретизации, установленным на 3.

III. МЕТОДИКА ЧИСЛЕННОЙ ХАРАКТЕРИСТИКИ

В этой статье мы стремимся дополнить, а не заменить, теоретические потери, изложенные в разделе II-A, путем цифрового расчета коэффициентов F и G для литцендратных конструкций. Цель состоит в том, чтобы позволить существующим правилам проектирования и процедурам оптимизации, (2) для круглых сплошных проводников (и/или идеализированного многожильного провода), и расширить область понимания и на многожильные провода без существенных модификаций. Более того, если диапазон коэффициентов F и G вычисляется для многих конфигураций литцендратной проволоки, то многожильная конструкция может быть добавлена в оптимизацию и проектирование в качестве дополнительного независимого параметра конфигурации.

Чтобы ограничить объем этой статьи, мы сосредоточим наше внимание на литцендрате круглого сечения. Отметим, что представленные методики имеют широкое применение литцендрата всех конструкций; например, литцендраты квадратного сечения были проанализированы и экспериментально подтверждены в [7].

А Конструкция и моделирование литцендрата

Круглые литцендраты наматываются путем рекурсивного скручивания пучков жил вместе на нескольких уровнях. На самом нижнем, самом внутреннем уровне находится небольшое количество тонких нитей, которые скручены спиралевидно. Осевое расстояние, пройденное за один полный оборот, известно как шаг спирали крутки. Затем скручивание рекурсивно повторяется на жгутах, чтобы сформировать многоуровневую структуру скрученной проволоки, как до этого мы показывали на рис. 1.

Легко заметить, что что многоуровневая спиральная структура соответствует определению литцендрата, потому что каждая жила проволоки на самом низком уровне может занимать все радиальные и азимутальные позиции во всем пучке. Следовательно, каждая нить вынуждена нести одинаковую величину тока, таким образом, мы добиваемся постоянства плотности тока по всему пучку.

Обратите внимание, что просто скрученная проволока с одним уровнем крутки допускает азимутальное, но не радиальное перемещение, поэтому не соответствует строгому определению настоящего литцендрата.

Рисунок 4: Пять нитей AWG 38 закручены в: (a) 2 витка / см; (b) 10 витков/см. Изоляция спрятана.

Математическая модель описанной выше конструкции начинается с набора n равномерно расположенных спиральных дорожек, центральная ось которых следует по пути всего пучка проводов. Эти пути можно преобразовать в сплошные проводники, проследив круглое поперечное сечение по их длине.

В качестве альтернативы, каждый спиральный путь может быть принят в качестве центральной оси для меньшего m набора винтовых путей, что приводит к двухуровневой, nxm винтовой конструкции. На каждом отдельном уровне все n-дорожки имеют одинаковый радиус спирали R и шаг P, которые являются взаимозависимыми, если предположить, что провода уложены вместе так, что их изоляция соприкасается. Используя тригонометрию и многомерное исчисление, можно показать, что расстояние между соседними винтовыми путями равно.

где ψ минимальная спиральная разность фаз, данная в качестве решения к

где φ = 2π/n. Расстояние D будет минимальным до тех пор, пока соседние нити или пучки не соприкоснутся. Это означает, что для одноуровневого жгута за D принимается диаметр составляющих жил плюс изоляция, а для заданного шага P значение R находится путем решения (3). Точно так же для многоуровневого пучка D устанавливается равным диаметру пучка на один уровень ниже, и соответственно определяется c помощью R. Реализация этого соотношения между D и P позволяет произвольно устанавливать шаг проволоки, сохраняя при этом плотный контакт между всеми соседними жилами.

B. Характеристика

В этом разделе мы кратко представляем обсуждение, в котором мы подразумеваем, что электромагнитная задача уже была сопоставлена с задачей эквивалентной схемы с использованием метода эквивалентной схемы с частичным элементом. Детали читатель может найти в [7], [12], [13]. Полную программу и исходный код можно найти в [18].

Коэффициент F, или коэффициент постоянного/переменного тока вычисляется с использованием стандартных методов извлечения полного сопротивления [13], [14]. Во-первых, частотно-зависимое сопротивление получается путем подачи синусоидального напряжения на сегмент эквивалентной схемы и вычисляется чистый ток. Разделив сопротивление постоянного тока получаем F. G, или коэффициент эффекта близости, получаем, подвергая модель сегмента воздействию изменяющегося во времени магнитного поля по его объему, при этом его пиковая величина нормализована до 1 А/м. По закону Фарадея это индуцирует напряжение вокруг каждой петли тока.

где l — длина петли, S — площадь петли, nˆ — вектор нормали. Если для решения эквивалентной схемы используется анализ сетки, то мы можем перебрать каждую петлю сетки и вычислить индуцированное напряжение. Распределение тока вычисляется путем решения задачи эквивалентной схемы, а потери мощности вычисляются путем суммирования i2R на каждом резисторе. Затем коэффициент G определяется как общие потеря, поделенная на длину проводника.

IV. ПРИМЕР ИЗ ПРАКТИКИ

В этом разделе мы представляем конкретный пример, основанный на процедурах, описанных выше, чтобы проиллюстрировать возможности метода и раскрыть некоторые идеи по конструкции литцендратной проволоки. Как подытожено ранее, проектные степени свободы для скрученной спиральной конструкции из литцендрата:

Диаметр жилы и толщина изоляции,
Количество прядей или пучков на каждом уровне и
Шаг спирали на каждом уровне, который может идти как по часовой, так и против часовой стрелки.

Из-за нехватки места мы сосредоточим наш анализ на третьей степени свободы, которая представляет собой шаг спирали. Поскольку уже существует большое количество литературы по оптимизации для первой степени свободы, мы привязываем наш анализ ниже к магнитному проводу калибра AWG 38 с диаметром 101 мкм и толщиной изоляции около 15 мкм. Количество прядей на каждом уровне установлено 5, а длина отрезка проволоки 2 см.

A. Одноуровневые охваты

Начинаем с одного уровня скручивания. На рис. 5 показана развертка общего сопротивления и коэффициента F в зависимости от частоты и количества витков в сегменте провода. Сразу видно, что увеличение числа витков увеличивает постоянную. сопротивления, тем самым компенсируя преимущества в улучшении F. Как обсуждалось в разделе II-A, одноуровневая конструкция не выигрывает от радиальной транспозиции, и поэтому отдельно ее потери не уменьшаются значительно с увеличением числа поворотов.

Однако, скручивание уменьшает потери из-за эффекта близости, как показано на рис. 6. При частоте 10 кГц это снижение составляет серьезные 90% по сравнению с нескрученным проводом, но преимущества исчезают с увеличением частоты. Мы можем увидеть объяснение этих результатов, заметив, что, когда многожильный провод помещен в магнитное поле, индуцируются два режима течения вихревых токов:

внутренние вихревые токи, которые циркулируют от пучка к пучку несут большие на более низких частотах; а также
внутренние вихревые токи, которые циркулируют в теле каждого проводника и потери преобладают на более высоких частотах.

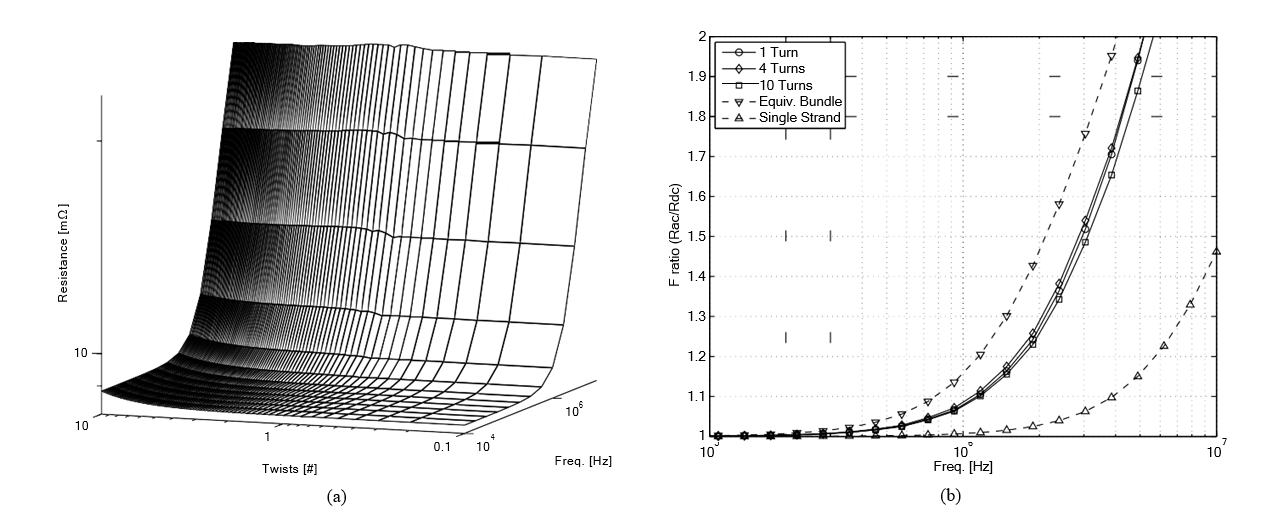
Рисунок 5: Пятипучковый закрученный проводник: (a) Сопротивление; (b) Коэффициент F. Частота от 10 кГц до 10 МГц. Количество витков от 0.25 до 10, с шагами 0.25 и 0.5.

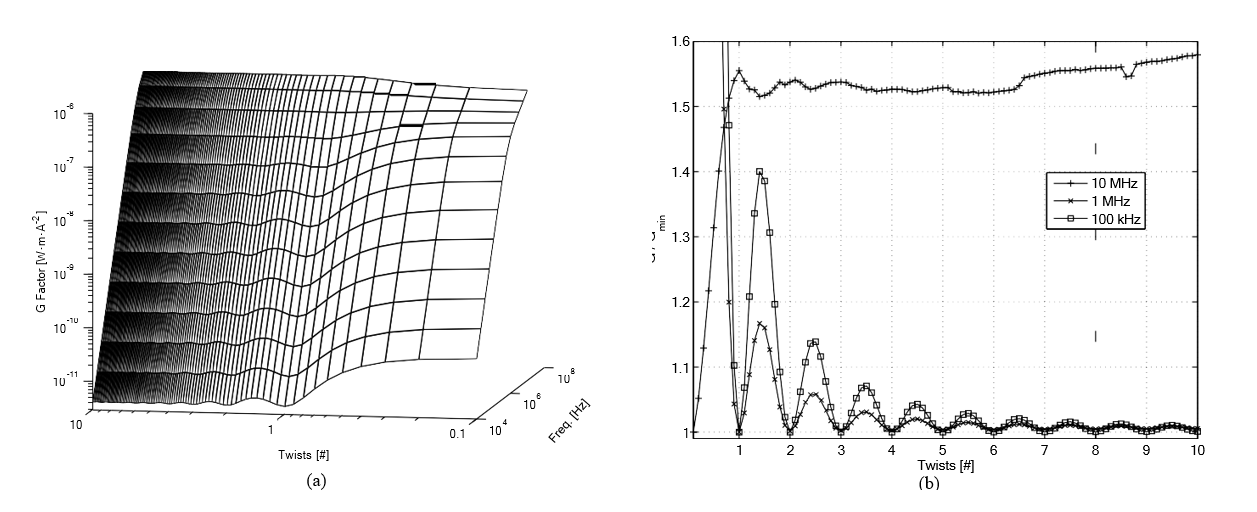
Рисунок 6: Пятипучковая закрученная проволока c коэффициентом G эффекта близости: (a) Чертеж пространства; (b) Приведенный к минимуму для каждой частоты. Частота от 10 кГц до 100 МГц. Количество закрутов от 0.1 до 10, с шагом 0.1.

перемещение, которое происходит благодаря закручиванию провода, позволяет потокосцеплению, связанному с вихрями внутри проводника, взаимодействовать между собой и полностью компенсироваться, когда в магнитном поле имеется целое число закручиваний. И остается небольшое количество внутрипроводниковых вихревых токов, которые несут потери. Однако, стратегия становится неэффективной, когда начинают доминировать внутренние вихри, особенно на более высоких частотах. В этих случаях потери уменьшаются за счет минимизации количества проводников, располагающихся поперек магнитного поля.

B. Двухуровневая закрученная пятинитка

Теперь мы рассмотрим двухуровневую структуру 5x5 с 25 нитями. Здесь нам особенно важно знать внутренний шаг. Он может быть:

Начальный шаг перед скручиванием, определяемый с использованием второго уровня в качестве системы отсчета; или же
Окончательный шаг после построения второго уровня, определяемый относительно глобальных координат.

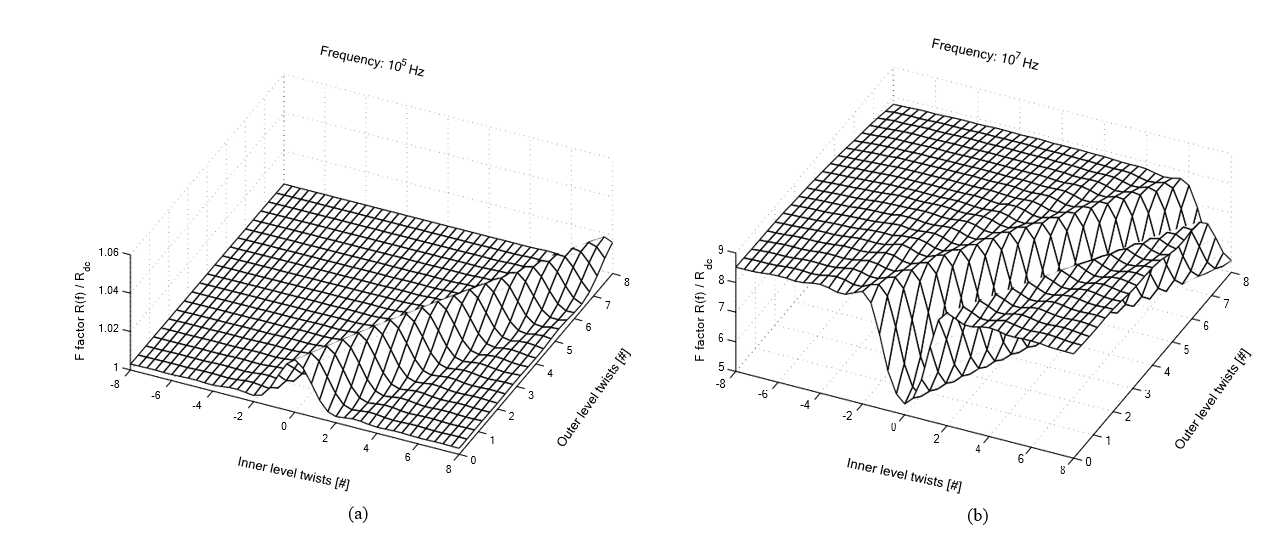
Рисунок 7: Коэффициент F двухуровневого литцедрата охватывает частоту внутреннего уровня и внешнего уровня с шагом 0,2 витка: (a) f = 100 кГц; (б) f = 10 МГц.

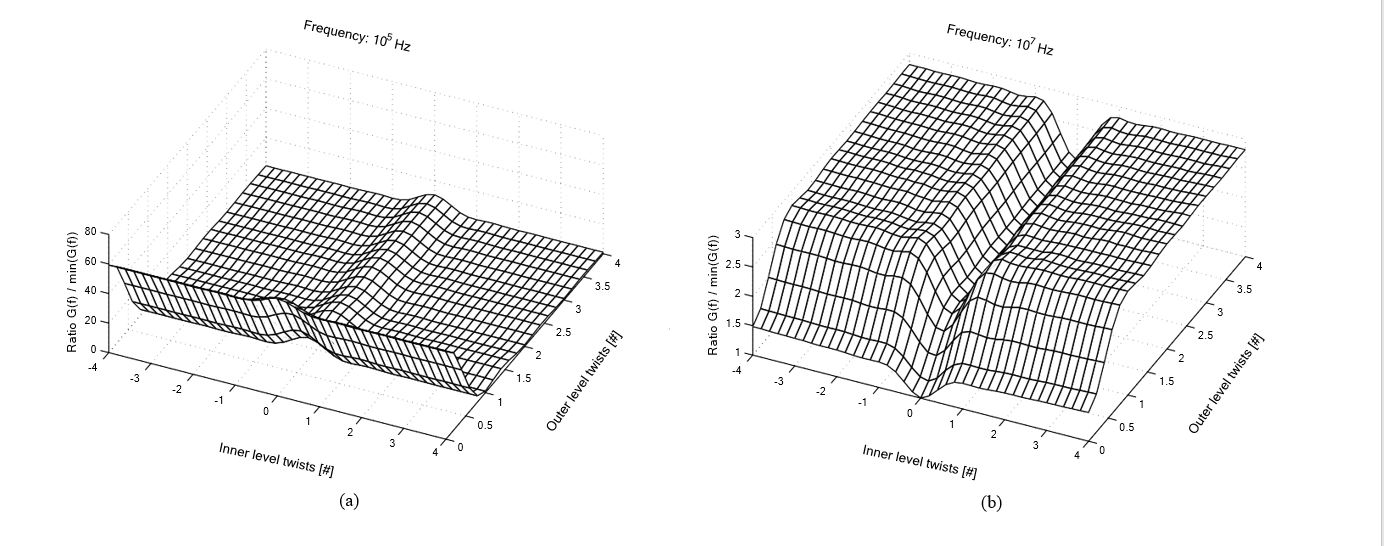
Рисунок 8: Коэффициент G двухуровневого литцедрата охватывает внутренний уровень и внешний шаг скрутки с шагами 0.2 витка: (a) f = 100 кГц; (b) f = 10 МГц.

Рисунок показывает второй случай, хотя они оба будут рассматриваться в дальнейшем обсуждении. Добавим, что число поворотов против часовой стрелки мы обозначаем положительным числом, а повороты по часовой стрелке — отрицательным числом. На рис. 7 показана развертка коэффициента F на двух частотах: 100 кГц и 10 МГц. Для каждого составного пучка внутреннего уровня внешнее магнитное поле, которое он испытывает, обусловлено соседними пучками.

Внешнее магнитное поле нормально распространяется к винтовой траектории внешнего уровня. Можно сказать, что высокие потери возникают там, где внутренний уровень имеет нулевую крутку относительно внешнего уровня, что соответствует определению первому случаю. Образуется диагональ по второму случаю, внутренний шаг равен внешнему шагу. По сути, эти провода ведут себя как одноуровневые 25-жильные провода, а не как двухуровневые пучки 5x5. Главная диагональ сопровождается впадинами, отстоящими на целое число закрутов в обе стороны. Это случаи, когда внутренний уровень имеет целое число поворотов относительно внешнего уровня, так что эффекты внутренней близости минимальны.

Вертикальная ось нормализована относительно минимального значения по всем охватам для этой частоты.

На рис. 8 показан тот же охват для коэффициента G. При этом внешние магнитные поля теперь однородны по глобальным координатам, что соответствует определению. Линии нулевого скручивания с большими потерями теперь проходят по осям относительно глобальных координат. Опять же, целое число витков дает наименьшие потери на частоте 100 кГц, снижая потери из-за близости до 60. Эта тенденция на высоких частотах становится обратной по тем же причинам, что и в одноуровневом случае.

С. Выводы

Скручивающаяся конструкция на каждом уровне снижает потери этого из-за внешних магнитных полей, не оказывая существенного влияния на потери от проводимости внутри жгута. Таким образом, у нас есть два простых решения по выбору длины шага в многоуровневом литцендрате:

Целое число витков оптимально минимизирует потерю эффекта близости. Избегайте использования менее 1 витка провода.
Для многоуровневых конструкций магнитные поля с эффектом близости возникают как внутри литцендрата, так и снаружи. Следовательно, для минимизации F в двухуровневой конструкции внутренний уровень должен иметь целочисленные закрутки относительно внешнего уровня, а для минимизации G оба уровня должны иметь целочисленные закрутки относительно глобальной оси.

Становится ясно, что одно и то же основное правило определяет минимизацию потерь во всех случаях, хотя и в разных системах координат, против магнитных полей, протекающих в разных направлениях.

Общие потери намного выше, чем допустимо для > 1 МГц. Хотя эти результаты включены для иллюстрации соответствия теории, они в значительной степени игнорируются при проектировании литцендрата.

V. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА

Чтобы подтвердить, что прогнозы моделирования соответствуют действительности, мы построили несколько многожильных проводов с различными калибрами жил, шагом, количеством жил и количеством уровней. На этом этапе было обнаружено, что спиральная модель в разделе III-A структурно несостоятельна для более чем трех прядей и будет иметь тенденцию разрушаться в гексагональную при растяжении. Следовательно, для обеспечения соответствия расчетной модели экспериментальному образцу была выбрана конструкция из трехжильного литцендрата.

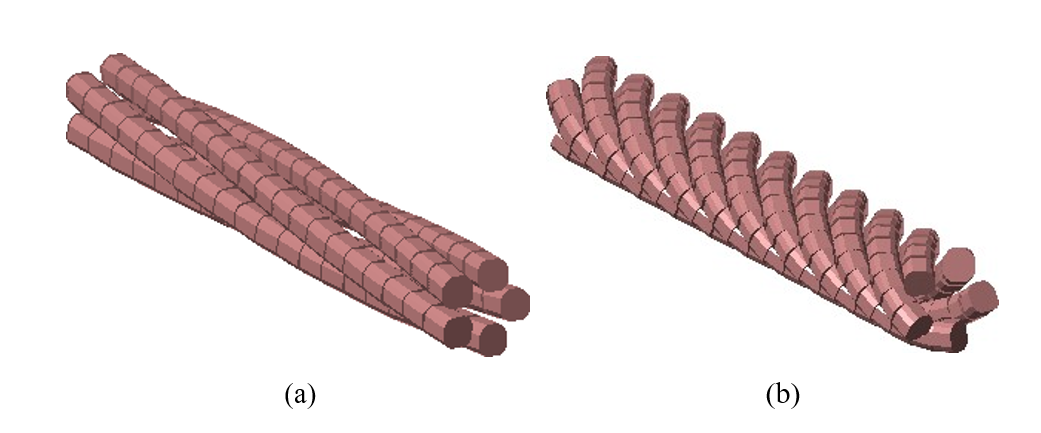
Во-первых, трехжильный скрученный жгут длиной 66 см с шагом спирали 10,05 см был изготовлен из проводов AWG 32 диаметром 202 мкм и толщиной изоляции около 30 мкм. Затем этот пучок был скручен в проволоку длиной 19 см и длиной 3,3 м, с шагом спирали, установленным на 10,04 см в противоположном направлении. Последняя конструкция вместе с расчетной моделью показана на рис. 9. Полное сопротивление клемм измеряли с помощью низкочастотного анализатора импеданса Agilent 4192A с проводами, уложенными зигзагообразно, змеевидно, чтобы свести к минимуму индуктивность и потери из-за эффекта близости. Резонансная пиковая характеристика наблюдалась в обоих наборах измерений; 60 пФ параллельной емкости было оценено методом наименьших квадратов по большому набору данных и соответствующим образом удалено. Аналитические прогнозы были сделаны с использованием уравнения (5) из [10].

Рисунок 9: Масштабное сравнение расчетной модели и фактического испытанного литцендрата

Как численный, так и аналитический методы дали отличные результаты измерений для трехжильного жгута на рис. 10а, особенно в области частоты колена 100–300 кГц, которая представляет собой диапазон, представляющий наибольший практический интерес для проектировщика. За пределами этого диапазона точность численного моделирования ухудшается. Это ожидаемый результат при использовании крупной сетки в проводнике после обсуждения в разделе II-B.

Результаты для провода 3x3 показаны на рис. 10b. Аналитическое решение значительно занижает сопротивление провода, поскольку оно предполагает идеальную литцевую конструкцию, в которой плотность тока совершенно одинакова в каждой жиле. По сравнению с этим цифровое решение подходит лучше, так как позволяет избежать этого предположения и явно моделировать неидеальную конструкцию провода. Тем не менее, посадка хуже, чем раньше. Из рис. 9 видно, что экспериментальный образец имеет дефекты изготовления. В частности, внутренний уровень частично разматывался неконтролируемым образом за счет скручивания внешнего уровня. Физические различия между расчетной моделью и экспериментальным образцом проволоки могут объяснить несоответствие между предсказаниями и измерениями.

VI. ВЫВОДЫ И ДАЛЬНЕЙШАЯ РАБОТА

Была представлена процедура определения характеристик скин-эффекта и потерь из-за эффекта близости с помощью быстрой цифровой процедуры оценки качества. Эксперименты, описанные в данной статье, позволяют убедиться в возможностях применения метода цифровой симуляции для усовершенствования конструкции литцедрата и являются доказательством его вычислительной эффективности. Однако эффективность и прогностическая способность нашего исследования еще сильно зависят от реалистичности самой вычислительной модели. Таким образом, естественным продолжением этой работы является адаптация цифровых методов для повышения точности моделирования литцендрата.

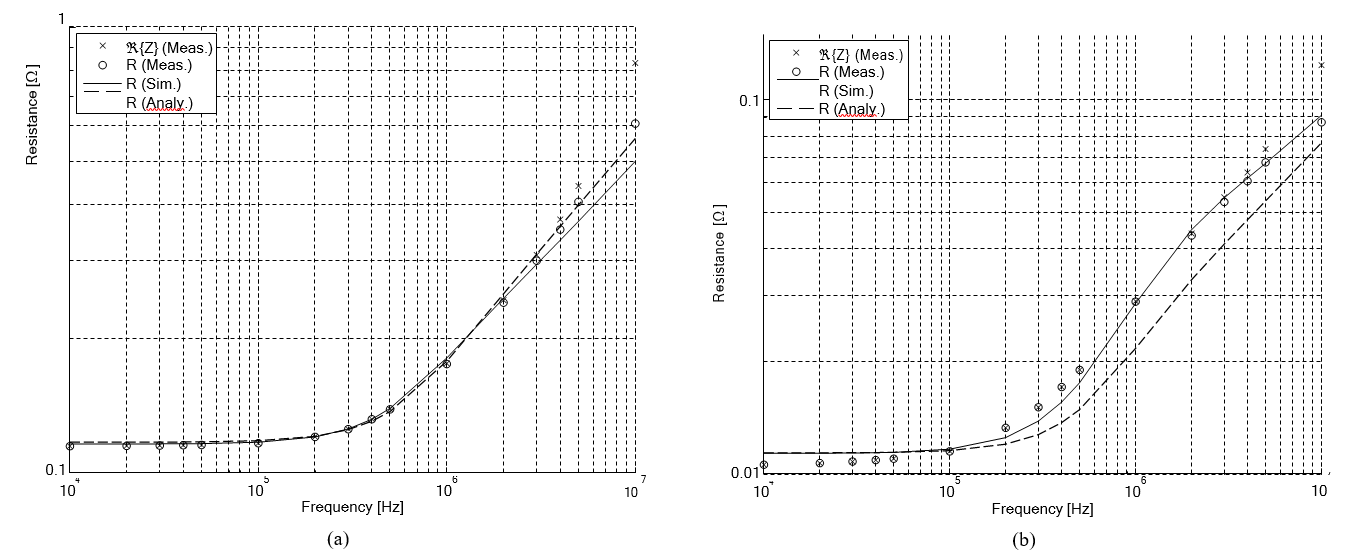
Рисунок 10: Сравнение измеренных и прогнозируемых сопротивлений для (а) одной пряди провода 3 × AWG калибра 32 и (b) двухуровневый литцедрата, изготовленного из проводов 3×3× AWG 32. Измеренное сопротивление, полученное путем удаления распределения на 60 рF (Power Factor(?) – прим. пер.) параллельная емкость от <{Z}. Аналитическое решение взято из [10].

Источники

[1] C. Sullivan, “Cost-constrained selection of strand diameter and num- ber in a litz-wire transformer winding,” IEEE Transactions on Power Electronics, vol. 16, no. 2, pp. 281–288, Mar. 2001.

[2] X. Tang and C. Sullivan, “Stranded wire with uninsulated strands as a low-cost alternative to litz wire,” in Proc. IEEE PESC’03, vol. 1, 2003, pp. 289–295.

[3] H. Rossmanith, M. Doebroenti, M. Albach, and D. Exner, “Measurement and Characterization of High Frequency Losses in Nonideal Litz Wires,” IEEE Transactions on Power Electronics, vol. 26, no. 11, pp. 3386–3394, Nov. 2011.

[4] P. Reddy, T. Jahns, and T. Bohn, “Transposition effects on bundle proximity losses in high-speed PM machines,” in Proc. IEEE ECCE’09, Sep. 2009, pp. 1919–1926.

[5] C. Sullivan, “Optimal choice for number of strands in a litz-wire transformer winding,” in Proc. IEEE PESC’97, vol. 1, 1997, pp. 28– 35.

[6] J. Acero, R. Alonso, J. Burdio, L. Barragán, and D. Puyal, “Frequency- dependent resistance in litz-wire planar windings for domestic induction heating appliances,” IEEE Transactions on Power Electronics, vol. 21, no. 4, pp. 856–866, 2006.

[7] R. Zhang, J. White, and J. Kassakian, “Fast simulation of complicated 3D structures above lossy magnetic media,” IEEE Transactions on Magnetics, to be published.

[8] J. Ferreira, “Improved analytical modeling of conductive losses in magnetic components,” IEEE Transactions on Power Electronics, vol. 9, no. 1, pp. 127–131, 1994.

[9] P. Dowell, “Effects of eddy currents in transformer windings,” Proceed- ings of the IEEE, vol. 113, no. 8, pp. 1387–1394, 1966.

[10] J. Ferreira, “Analytical computation of AC resistance of round and rectangular litz wire windings,” Electric Power Applications, IEE Pro- ceedings B, vol. 139, no. 1, pp. 21–25, 1992.

[11] N. McLachlan, Bessel functions for engineers. Oxford: Clarendon Press, 1955

[12] A. Ruehli, “Equivalent Circuit Models for Three-Dimensional Mul- ticonductor Systems,” IEEE Transactions on Microwave Theory and Techniques, vol. 22, no. 3, pp. 216–221, Mar. 1974.

[13] M. Kamon, M. Ttsuk, and J. White, “FASTHENRY: a multipole- accelerated 3-D inductance extraction program,” IEEE Transactions on Microwave Theory and Techniques, vol. 42, no. 9, pp. 1750–1758, 1994.

[14] A. E. Ruehli, “Inductance Calculations in a Complex Integrated Circuit Environment,” IBM Journal of Research and Development, vol. 16, no. 5, pp. 470–481, Sep. 1972.

[15] W. T. Weeks, L. L.-H. Wu, M. F. McAllister, and A. Singh, “Resistive and Inductive Skin Effect in Rectangular Conductors,” IBM Journal of Research and Development, vol. 23, no. 6, pp. 652–660, Nov. 1979.